Техническое описание программы "Модула"

В процессе криптографических расчетов очень часто приходится решать сравнения, тоесть модульные уравнения
вида: А*j = x mod p, Причем р обычно заранее известно, j нужно найти, а величины А и х можно подставлять произвольно.
Либо заранее могут быть заданы величины А и х, а перебирать можно j.
В криптографии обычно такие уравнения решают с использованием алгоритма Евклида, который обладает
100% - ной доказанной сходимостью. Но для прикидочных расчетов, которые обычно встречаются в студенческой практике,
алгоритмом Евклида пользоваться не всегда удобно.
Особенно это становится заметно, когда модули не слишком большие,
а адаптировать алгоритм Евклида под конкретную вычислительную задачу не очень хочется.
Именно для таких случаев я написал этот калькулятор, который позволяет решать подобные уравнения прямым перебором.
Благо мощность современных компьютеров вполне позволяет заниматься подобными вещами.
Поскольку алгоритм Евклида в нем не используется, никаких гарантий сходимости он разумеется дать не может.
Однако практика показывает, что если задать достаточно большое значение j, то решение сравнения достигается в 90%
случаев.
Порядок использования следующий.
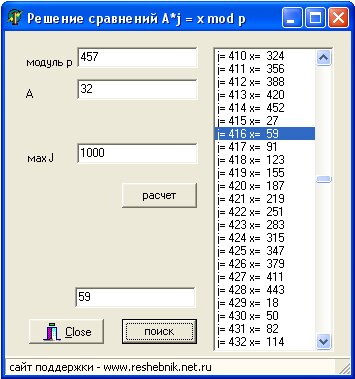
1. Вначале задаем модуль р и величину А. Потом определяемся с количеством перебираемых вариантов j.
Величина j определяется только вашей фантазией и объемом памяти компьютера, однако чем большую величину вы задаете,
тем сильнее компьютер будет задумываться :))
2. Нажимаем кнопку "расчет", затем в окошке "искомое число" задаем искомое значение х. Если среди различных вариантов
решения данного сравнения встречается такой х, то программа его находит и показывает выделением строки.
Если такого решения нет, выбрасывается соответствующая табличка.
В этом случае можно попробовать увеличить количество вариантов перебора j.
 kennobi 16.05.2010г.
kennobi 16.05.2010г.
Комментарии пользователей:
| Valeria | 2012-04-12 10:45:53 |
| When you think about it, that\'s got to be the right anwesr. |
| Mahaley | 2016-10-22 01:16:49 |
| Deep thought! Thanks for cotbrinuting. |




 В процессе криптографических расчетов очень часто приходится решать сравнения, тоесть модульные уравнения
вида: А*j = x mod p, Причем р обычно заранее известно, j нужно найти, а величины А и х можно подставлять произвольно.
Либо заранее могут быть заданы величины А и х, а перебирать можно j.
В процессе криптографических расчетов очень часто приходится решать сравнения, тоесть модульные уравнения
вида: А*j = x mod p, Причем р обычно заранее известно, j нужно найти, а величины А и х можно подставлять произвольно.
Либо заранее могут быть заданы величины А и х, а перебирать можно j.